Circuit couplé
I . Introduction :
L’étude d’un système qui a un mouvement vibratoire à oscillations sinusoïdales se démontre en fonction du temps .
Pour cela en va étudier des systèmes sous l’action d’une pulsation électrique .
II . But :
Le but de ce TP est de déterminer le type de couplage électrique .
III . Etude et manipulation :
1.Circuit oscillant :
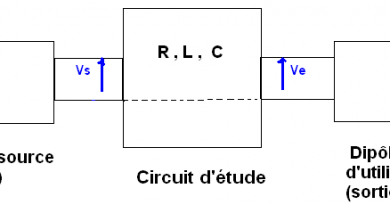
On fait le montage du circuit RLC oscillant pour toute notre expérience , on règle la tension efficace à ( E = 1 Volt ) avec l’oscilloscope .
On rappel que la tension cret-cret Ecc = 2.Emax = 2 E √2 .
Les condensateurs sont choisit C = 1nf .
On fait varier la fréquence et on note l’intensité du courant , les résultat sont données par le tableau ci-dessous :
| F(KHz) | 40 | 42 | 44 | 46 | 48 | 50 | 52.5 | 55 | 57.5 | 60 |
| I(mA) | 0.7 | 0.8 | 1 | 1.4 | 1.9 | 2.5 | 2.3 | 1.4 | 0.9 | 0.7 |
a)- la courbe I = f(f) :
b)- On déduire la fréquence de résonance f0 et Imax :
D’après le tableau et le graphe I = f(f) c’est :
f0 = 50 KHz → I = 2.5 mA
c)- On mesure la bande passante :
Mesurer sur le graphe la largeur de la bande passante B = f2 – f1
à 3 décibels ,
(f1 et f2 étant les fréquences correspondantes au courant I = Imax / √2).
D’après le graphe au point de I = Imax /√2
I = 2.5 /√2 = 1.77 mA
On à deux valeurs de fréquence d’après le graphe :
.f1 = 46.3 KHz
.f2 = 53.2 KHz
B = f2 – f1 ⇒ B = 53.2 – 46.2 = 6.9 KHz
d)- Le coefficient de qualité :
On rappel le coefficient de qualité du circuit :
Q = f0 / B
AN :
Q = 50 / 6.9
Q = 7.24
e)- L’inductance L et la résistance :
Q = f0 / B = 1 / RCω0 = L ω0 /R
Avec ω0 = 2πf0
A la résonance LCω0² = 1
⇒ L = 1 / Cω0²
⇒ L = 1 / C (2πf0)²
⇒ L = 1 / 10-6 . ( 2 . 3.14 . 50 )²
⇒ L = 10.14
on a : R = L ω0 / Q
R = 10.14 . ( 2 . 3.14 . 50 ) / 7.24
R = 439.77 Ω
2. circuit couplé :
On fait le montage du circuit couplé , on fixe la fréquence du circuit forcé
L-C a sa fréquence de résonance (f0 = 50).
On branche l’oscilloscope aux bornes de C’ du circuit libre L’-C’ pour la mesure de la tension Vcc entre ses bornes .
(C’ = C = 1nF ; les bobines sont identiques ).
Pour différentes distances ‘d’ séparant les bobines , mesurer Vcc :
| D(cm) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Vcc(Volt) | 8.2 | 7.0 | 5.5 | 4.5 | 3.8 | 3.0 | 2.5 |
Voici le graphe Vcc = f(d) :
conclusion :
d’après le graphe [Vcc = f(d)] et le tableau on remarque que la différence de potentiel (ddp) entre les bornes de CC diminue suivant la distance entre les deux bobines ,chaque fois que la distance et grande la (ddp) diminue et pour une distance égale à zéro on a la (dpp) aux maximum c’est à dire [ la distance entre les bornes d(cm) augmente implique que la différence de potentiel entre les bornes Vcc diminue ].
– On rajoute un Ampère mètre au circuit L’- C’ et on mesure les différents courant des deux circuit (L – C) et ( L’ – C’ ) :
| f(KHz) | 40 | 42 | 44 | 46 | 48 | 50 | 52.5 | 55 | 57.5 | 60 |
| I1 | 0.6 | 0.7 | 0.9 | 1.3 | 1.7 | 2.1 | 1.9 | 1.3 | 0.9 | 0.7 |
| I2 | 0.04 | 0.06 | 0.07 | 0.09 | 0.16 | 0.28 | 0.32 | 0.28 | 0.17 | 0.05 |
| I1+I2 | 0.64 | 0.76 | 0.97 | 1.39 | 1.86 | 2.38 | 2.22 | 1.58 | 1.07 | 0.75 |
Voici le graphe (I1+I2) = f(f) :
– on trace la courbe (I1+I2) = f(f) avec l’autre courbe I = f(f)
on remarque que [ I ] et [ I1+I2 ] sont égaux à peut prés, même on remarque d’après la courbe [ I =f(f) et (I1+I2) = f(f)] que les courbes I =f(f) et (I1+I2) = f(f) sont à peut prés les mêmes .
3. Une mesure de la mutuelle inductance M :
On fait le montage du circuit série . On fera (d = 0) , c’est à dire coller les bobines montés en série l’une contre l’autre .
Premier temps :
Le courant circule dans le même sens dans les enroulements des deux bobines , les flux (Ldi/dt) et (Mdi/dt) sont additifs et à la résonance on montre que :
L + M = ½ Cω1²………..(1)
fréquence de résonance f1 = 34 KHz mode 1.
deuxième temps :
croiser les connexions A et B de l’une des bobines , les courants dans les enroulements des bobines circulent alors en sens contraire , les flux sont ainsi soustractifs et à la résonance on montre que :Si vous êtes à la recherche de superclones Replica Rolex , Super Clone Rolex est l’endroit où aller ! La plus grande collection de fausses montres Rolex en ligne !
L – M = ½ Cω2²..…..….(2)
Fréquence de résonance f2 = 38 KHz mode 2 .
*On déduire M à partir du système d’équations (1) et (2) :
ω = 2πf donc : ω1=2πf1= 213.52KHz
ω2=2πf2= 238.64KHz
Déduire M :
(1) + (2) ⇒ 2L = ½ C ω1² + ½ C ω2²
⇒ L = 9.87
(1) – (2) ⇒ 2L = ½ C ω1² – ½ C ω2²
⇒ M = 1.09
Déduire K:
K = M / L
A .N :
K = 1.09 / 9.87
K = 0.11
On a :
1 / Q = 0.138 (d’après la première question)
4 . CONCLUSION :
Couplage :
Lâche Critique Serré
1 / Q
D’après les résultat obtenus on arrive à déduire le type de couplage de ce circuit , car puisque K = 1 / Q alors le couplage est CRITIQUE .