Le Théorème de Thévenin
Introduction
Le Théorème de Thévenin est une propriété électronique, qui établit qu’un réseau électrique linéaire vu de deux points est équivalent à un générateur parfait dont la tension est égale à la différence de potentiels à vide entre ces deux points, en série avec une résistance égale à celle que l’on mesure entre les points lorsque les générateurs indépendants sont rendus passifs.
Ce théorème a été initialement découvert par le scientifique Allemand Hermann von Helmholtz en 1853, puis en 1883 par l’ingénieur télégraphe français Léon Charles Thévenin.
But
Remplacer un circuit complexe par un circuit composé d’une source de tension et une résistance
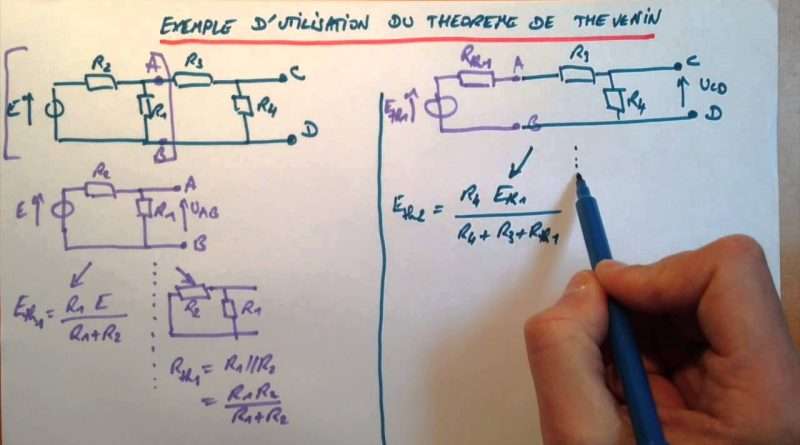
Équivalent de Thévenin
Identifier les bornes du circuit et la charge externe
Mesurer ou calculer la tension au borne du circuit sans charge extérieur c est la tension de Thévenin
Annuler les sources et déterminer la résistance vue des bornes du circuit d’est la résistance de Thévenin
Théorème de Thévenin
Annuler une sources de tension consiste a la remplacer par un court_circuit
Annuler de courant (circuit ouvert)
Matériel Utiliser :
- GBF.
- Oscilloscope.
- 02 résistances : 47 et 1k Ohm.
- 01 condensateur de capacité 0.47 micro farad.
Travail demandé
- Réalisation de montage (sans la résistance variable R)
- Pour cette question il suffit de réaliser notre tentions d’entrer ( générateur ) a laid de l’oscilloscope et on trouve que e(t)=2Vsur le canal 1 et pour la sortie VAB=1.6V sur le canal 2 .
On a trouver l’amplitude ∆T=0.004 et le déphasage
ϕ=25.12°
Puisque le circuit sans la charge( a vide ) on trouve que V0 correspond bien a VAB presque le courant qui traverse R2 est nul .
Calculer théoriquement V0 et U
Calculer V0
On appliqué le diviseur de tension
VAB = V0 =1.8V ~VAB pratique
Calculer ϕ
On a
cosϕ=
sinϕ= tgϕ=R1cw
ϕ = arctg (R1cw)
ϕ = 27.97°
ϕthéorique = ϕpratique
- on branche une résistance de 100KΩentre A et B on varie R de 5Ω a 5KΩ
on a Vz=Rz*Iz Iz=Vz/R
f=1KH
| R Ω | 5 | 10 | 30 | 60 | 200 | 500 | 1K | 5K |
| VR | 0.009 | 0.007 | 0.02 | 0.05 | 0.1 | 0.2 | 0.24 | 0.24 |
| Iz | 1.8 | 0.7 | 0.66 | 0.58 | 0.5 | 0.4 | 0.24 | 0.05 |
| ∆T | 0 | 0.04 | 0.1 | 0.06 | 0.08 | 0.1 | 0.12 | 0.16 |
| ϕ | 0 | 0.25 | 0.62 | 0.37 | 0.5 | 0.62 | 0.75 | 1 |
Mesure de l’impédance Z0
Calculer le courant I
La tension au bornes de la résistance R2 , V=0.98V
VR2=R2*I I = VR2/R2
I = 0.98/47
I = 0.02 A
Calcul de Z0 pratique
On a Ve =Z0*I
Et T= VR2/R2
Donc
Z0 = 95.91Ω
Calcul de Z0 théoriquement
On remarque que Z0theorique n’est égale pas Z0pratique a cause de l’erreur de mesure provoque par l’appareil
Les réponses de question
On montrer que l’expression
Peut s’écrire aussi parce que dans le théorème de Thévenin on a l’impédance de Z0 en série avec V0 est on applique la loi des mailles plus la loi d’ohm V0 = Z0*I0
Pour caque valeur Z=R1 on vérifie que
| R Ω | 5 | 10 | 30 | 60 | 200 | 500 | 1000 | 5000 |
| IZ | 0.03 | 0.027 | 0.02 | 0.0014 | 0.006 | 2.92 | 0.03 | 0.03 |
Conclusion :
Dans ce TP on a appris d’appliquer le théorème de Thévenin dans n’importe qu’elle circuit
On calculons d’abord Rth = Req dans un circuit ouvert sans charge puis on calcule Eth = V0
On éliminons toujours notre charge mais avant il nous faut le courant et pour ce la on peut appliquer plusieurs méthodes et après tous ca on rend notre charge et en remplace le premier circuit avec nos résultas (Rth , Eth et un nouveau courant).