GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
This paper (by Apple) questions the mathematical reasoning abilities of current LLMs and designs a synthetic template-based dataset distribution to investigate various aspects around LLM performance of high-school level math questions.
Paper: https://arxiv.org/abs/2410.05229
Abstract:
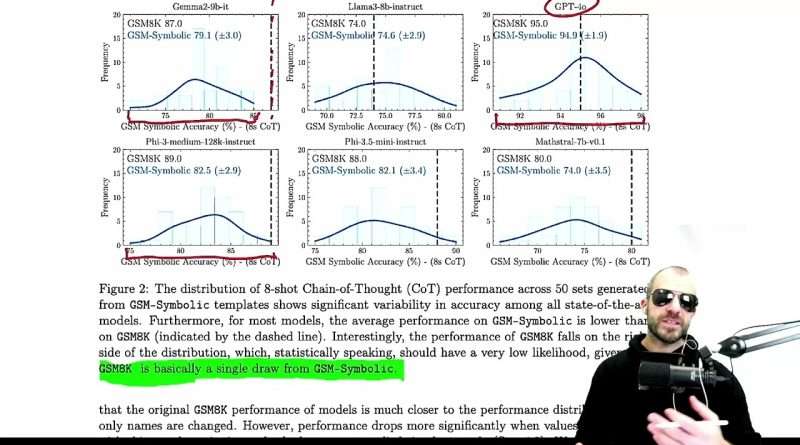
Recent advancements in Large Language Models (LLMs) have sparked interest in their formal reasoning capabilities, particularly in mathematics. The GSM8K benchmark is widely used to assess the mathematical reasoning of models on grade-school-level questions. While the performance of LLMs on GSM8K has significantly improved in recent years, it remains unclear whether their mathematical reasoning capabilities have genuinely advanced, raising questions about the reliability of the reported metrics. To address these concerns, we conduct a large-scale study on several SOTA open and closed models. To overcome the limitations of existing evaluations, we introduce GSM-Symbolic, an improved benchmark created from symbolic templates that allow for the generation of a diverse set of questions. GSM-Symbolic enables more controllable evaluations, providing key insights and more reliable metrics for measuring the reasoning capabilities of this http URL findings reveal that LLMs exhibit noticeable variance when responding to different instantiations of the same question. Specifically, the performance of all models declines when only the numerical values in the question are altered in the GSM-Symbolic benchmark. Furthermore, we investigate the fragility of mathematical reasoning in these models and show that their performance significantly deteriorates as the number of clauses in a question increases. We hypothesize that this decline is because current LLMs cannot perform genuine logical reasoning; they replicate reasoning steps from their training data. Adding a single clause that seems relevant to the question causes significant performance drops (up to 65%) across all state-of-the-art models, even though the clause doesn’t contribute to the reasoning chain needed for the final answer. Overall, our work offers a more nuanced understanding of LLMs’ capabilities and limitations in mathematical reasoning.
Authors: Iman Mirzadeh, Keivan Alizadeh, Hooman Shahrokhi, Oncel Tuzel, Samy Bengio, Mehrdad Farajtabar
Links:
Homepage: https://ykilcher.com
Merch: https://ykilcher.com/merch
YouTube: https://www.youtube.com/c/yannickilcher
Twitter: https://twitter.com/ykilcher
Discord: https://ykilcher.com/discord
LinkedIn: https://www.linkedin.com/in/ykilcher
If you want to support me, the best thing to do is to share out the content 🙂
If you want to support me financially (completely optional and voluntary, but a lot of people have asked for this):
SubscribeStar: https://www.subscribestar.com/yannickilcher
Patreon: https://www.patreon.com/yannickilcher
Bitcoin (BTC): bc1q49lsw3q325tr58ygf8sudx2dqfguclvngvy2cq
Ethereum (ETH): 0x7ad3513E3B8f66799f507Aa7874b1B0eBC7F85e2
Litecoin (LTC): LQW2TRyKYetVC8WjFkhpPhtpbDM4Vw7r9m
Monero (XMR): 4ACL8AGrEo5hAir8A9CeVrW8pEauWvnp1WnSDZxW7tziCDLhZAGsgzhRQABDnFy8yuM9fWJDviJPHKRjV4FWt19CJZN9D4n
Views : 13410
GSM